La sucesión de Fibonacci es una secuencia de números que podría parecer un sencillo ejercicio matemático. Sin embargo, su relación con la razón aúrea y, sobr.. Números Fibonacci (Secuencia): 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 . . . Los números Fibonacci (Los primeros 14 están listados arriba) son una secuencia de números definidos recursivamente por la fórmula F 0 = 1 F 1 = 1 F n = F n - 2 + F n - 1 donde n ≥ 2.

¿Sabías que...? sobre la sucesión de Fibonacci matematicascercanas

The Fibonacci sequence number of “1 000 000” One Million? ITArray

Diagrama de flujo Serie Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, YouTube

PHP fibonacci sequence Renato Lucena

La sucesión de fibonacci y la razón áurea by Víctor Calderón Issuu
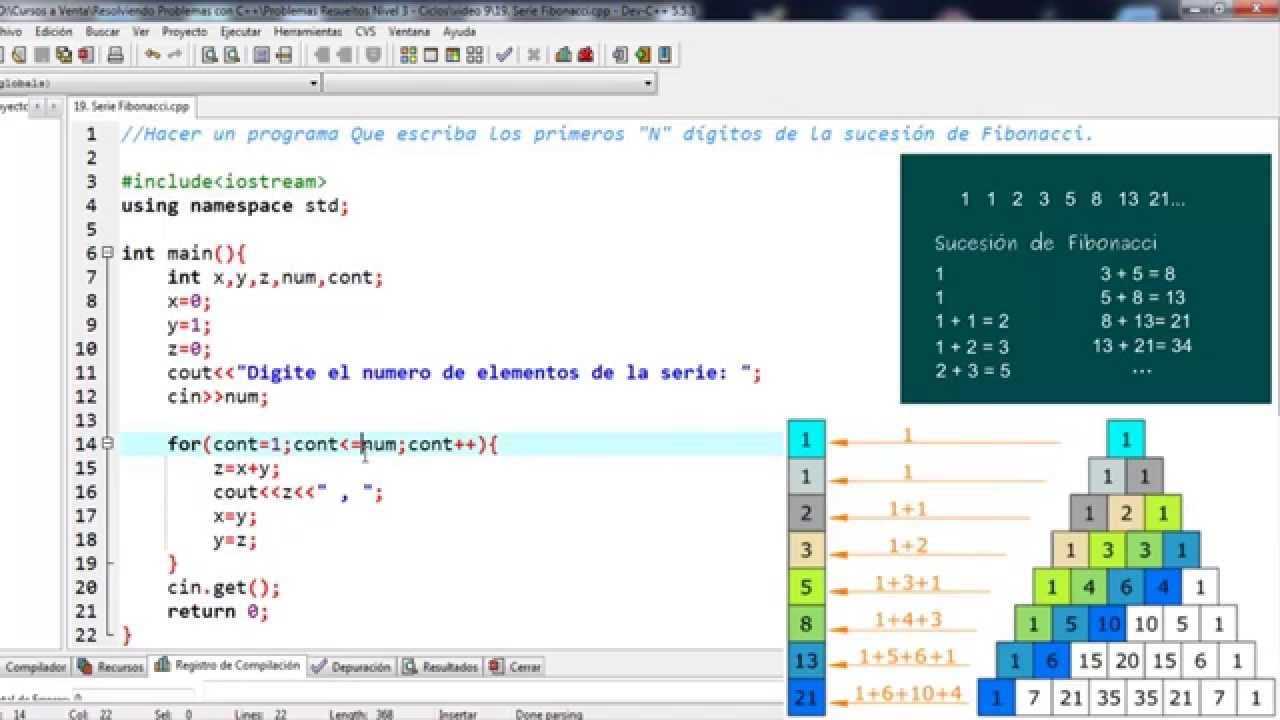
Programacioón en C y C++ Serie Fibonacci YouTube

¿Que es la sucesión de Fibonacci y como se construye? Mowna

secuencia fibonacci Secuencia de fibonacci, Ciencia y conocimiento, Ejercicios de dibujo

Fibonacci series in python program Technotaught

Render Illustration Fibonacci Series Script First Stock Illustration 1086667955 Shutterstock

¿Qué es la sucesión de Fibonacci? Todo sobre la fórmula de la naturaleza

¿Cómo funcionan los retrocesos de Fibonacci? CRIPTO TENDENCIA
Comment calculer la suite de Fibonacci avec Excel Formule Excel

¿Qué es la secuencia de Fibonacci y cómo se relaciona con la arquitectura? ArchDaily México

Qué es la serie de Fibonacci y qué tiene que ver con el número áureo BBC News Mundo

La sucesión de Fibonacci y sus propiedades Los Ojos del Júcar

Apa Itu Fibonacci Retracement Dalam Trading? Broker Forex Terbaik

La sucesión de Fibonacci y sus propiedades Los Ojos del Júcar

The calculator Lab MSX Files La sucesión de Fibonacci con un Toshiba HX10E

Fibonacci Forex Trading Explained
Serie de Fibonacci: Es la secuencia de números: 0,1,1,2,3,5,8,13,21,. Cada número es el resultado de la suma de los 2 números anteriores. Por lo tanto, después de 1 y 1, el siguiente número es 1+1=2, el siguiente es 1+2=3, el siguiente es 2+3=5 y así continúa.. Ver solución. Introducción a la sucesión de Fibonacci: concepto, fórmula por recurrencia, fórmula de Binet, algunas propiedades y problemas resueltos. Secundaria, ESO y Bachillerato.